FOODIE

"Fortran Object-Oriented Differential-equations Integration Environment, FOODIE.

Modern Fortran standards (2003+) have introduced support for Object-Oriented Programming (OOP). Exploiting new features like Abstract Data Type (ADT) is now possible to develop a KISS library providing an awesome environment for the numerical integration of Differential-equations such as Ordinary and Partial Differential Eqautions (ODE, PDE). FOODIE is tailored to the systems arising from the semi-discretization of PDEs, but it is not limited to them.
The FOODIE environment allows the (numerical) solution of general, non linear differential equations system of the form:



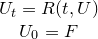
where:

• U_t = dU/dt;
• U is the vector of state variables being a function of the time-like independent variable t;
• R is the (vectorial) residual function, it could be a non linear function of the solution U itself;
• F is the (vectorial) initial conditions function.

FOODIE is aimed to be a KISS-pure-Fortran library for integrating Ordinary Differential Equations (ODE), it being:

• Pure Fortran implementation;
• KISS and user-friendly:
  • simple API, presently based on the Rouson's Abstract Data Type Pattern [8];
  • easy building and porting on heterogeneous architectures;
• comprehensive solvers set out-of-the-box:
  • explicit schemes:
    • Adams-Bashforth schemes see [7, 12]:
      • 1 step, namely the forward explicit Euler scheme, 1st order accurate;
      • 2 to 16 steps, 2nd to 16th accurate, respectively;
    • Euler (forward explicit) scheme, 1st order accurate;
    • Leapfrog, 2nd order accurate:
      • unfiltered leapfrog, 2nd order accurate, mostly unstable, see [4];
      • Robert-Asselin filtered leapfrog, 1st order accurate, see [4, 5, 6];
      • Robert-Asselin-Williams filtered leapfrog, 3rd order accurate, see [5, 6];
    • Linear Multistep Methods, SSP schemes see [16]:
      • 3 steps, 2nd order accurate;
      • 4 steps, 3rd order accurate;
      • 5 steps, 3rd order accurate;
    • Linear Multistep Methods, SSP with Variable Step Size (VSS) schemes see [17]:
      • 2 steps, 2nd order accurate;
      • 3 steps, 2nd order accurate;
      • 3 steps, 3rd order accurate;
      • 4 steps, 3rd order accurate;
      • 5 steps, 3rd order accurate;
    • Linear Multistep Runge-Kutta Methods SSP schemes see [18]:
      • 2 steps, 2 stages, 3rd order accurate;
      • 3 steps, 2 stages, 3rd order accurate;
      • 4 steps, 3 stages, 5th order accurate;
      • 3 steps, 6 stages, 5th order accurate;
      • 3 steps, 5 stages, 6th order accurate;
      • 3 steps, 7 stages, 7th order accurate;
      • 4 steps, 7 stages, 7th order accurate;
      • 4 steps, 5 stages, 8th order accurate;
      • 5 steps, 9 stages, 8th order accurate;
      • 4 steps, 9 stages, 9th order accurate;
      • 3 steps, 20 stages, 10th order accurate;
    • Runge-Kutta schemes:
      • [+] Linear SSP (of any order) schemes, see [16]:
        • generic s-stages of order (s-1)-th;
        • generic s-stages of order s-th;
      • low-storage schemes, see [1, 2, 3]:
        • 1 stage, namely the forward explicit Euler scheme, 1st order accurate;
        • 2 stages;
        • 3 stages;
        • 4 stages;
        • 5 stages, 4th order accurate, 2N registers, see [3];
        • 6 stages, 4th order accurate, 2N registers, see [9];
        • 7 stages, 4th order accurate, 2N registers, see [9];
        • 12 stages, 4th order accurate, 2N registers, see [10];
        • 13 stages, 4th order accurate, 2N registers, see [10];
        • 14 stages, 4th order accurate, 2N registers, see [10];
      • TVD/SSP schemes, see [1]:
        • 1 stage, namely the forward explicit Euler scheme, 1st order accurate;
        • 2 stages, 2nd order accurate;
        • 3 stages, 3rd order accurate;
        • 4 stages;
        • 5 stages, 4th order accurate;
      • embedded (adaptive) schemes:
        • Heun-Euler, 2 stages, 2nd order accurate;
        • Runge-Kutta-Fehlberg, 5 stages, 4th order accurate;
        • Runge-Kutta-Cash-Karp, 6 stages, 5th order accurate, see [13];
        • Prince-Dormand, 7 stages, 4th order accurate, see [11];
        • Calvo, 9 stages, 6th order accurate, see [14];
        • Feagin, 17 stages, 10th order accurate, see [15];
  • implicit schemes:
    • Runge-Kutta schemes;
    • Adams-Moulton schemes:
      • 0 step, 1st order accurate;
      • 1 step, 2nd accurate;
      • 2 steps, 3rd accurate;
      • 3 steps, 4th accurate;
    • Backward Differentiation Formula schemes:
      • 1 step, namely the backward implicit Euler scheme, 1st order accurate;
      • 2 to 6 steps, 2nd to 6th accurate, respectively;
  • predictor-corrector schemes:
    • Adams-Bashforth-Moulton schemes:
      • 1 step, AB(1)-AM(0), 1st order accurate;
      • 2 steps, AB(2)-AM(1), 2nd accurate;
      • 3 steps, AB(3)-AM(2), 3rd accurate;
      • 4 steps, AB(4)-AM(3), 4th accurate;
• efficient and non intrusive:
  • FOODIE environment is unaware of any eventual parallel paradigms the clients used, but it is proved to preserve high scalability on parallel architectures such as:
    • OpenMP directive-based codes on shared memory multi/many cores architectures;
    • CoArray Fortran (CAF) based codes for Partitioned Global Address Space (PGAS) programming model;
    • MPI based code on distributed memory clusters;
    • GPGPU/accelerators device enabled codes;
• Tests-Driven Developed (TDD):
• well documented:
  • clear documentation of schemes implementations, e.g. see Adams-Bashforth API documentation;
  • complete API reference;
  • comprehensive wiki:
• collaborative developed on GitHub;
• FOSS licensed

https://github.com/Fortran-FOSS-Programmers/FOODIE